Численное моделирование управления сверх- и гиперзвуковыми потоками с помощью локального подвода энергии

Карпенко А. Г.
Исследование поддержано РФФИ, проект № 16-38-60142, 2016 – 2018 гг.

При больших скоростях полета в плотных слоях атмосферы аэродинамические характеристики летательного аппарата, такие как коэффициенты сопротивления и моментов, перестают зависеть от числа Маха M. Коэффициент подъемной силы пластины резко уменьшается с ростом числа Маха и становится при гиперзвуковых скоростях очень низким. Поэтому управлять аппаратом становится сложнее. Одним из способов управления является локальный подвод энергии перед ЛА, например, с помощью СВЧ или лазерного разряда. При этом разрушается головная ударная волна или изменяется угол скачка уплотнения, модифицируется картина обтекания и меняются коэффициенты подъемной силы. При течении в полостях гиперзвуковых воздушно-реактивных двигателей (ГПВРД) с помощью локального подвода энергии можно изменять систему скачков и структуру течения. Этот механизм можно использовать для выведения из строя ГПРВД при противовоздушной обороне или для интенсификации сгорания топлива в нем. При больших скоростях полета температура газа в возмущенной области около тела сильно возрастает, поэтому свойства воздуха существенно отличаются от свойств совершенного газа. Начинают играть заметную роль возбуждение колебательных степеней свободы, процессы диссоциации, ионизации и неравновесность газа. Нагрев воздуха и сжатие его перед головной ударной волной может вызвать мощные потоки лучистой энергии, которые влияют на теплообмен и могут быть использованы для обнаружения ЛА.

Выполнена разработка программ расчета пространственных течений вязкого сжимаемого газа на неструктурированных сетках с учетом равновесных химических реакций. В разработанные методы расчета добавлен учет химических реакций в воздухе, которые происходят при гиперзвуковых скоростях полета. Рассматривается случай реагирующей смеси газов, состоящей из нейтральных и заряженных частиц. Все химические процессы в воздухе считаются равновесными, а воздух при этом считается смесью различных компонентов идеальных газов (N₂, O₂, NO, N, O, N⁺, O⁺, Ar, Ar⁺ и т.д.). Можно составить систему уравнений относительно мольных долей компонентов смеси, состоящую из закона сохранения вещества (сохранения атомов химических элементов), уравнения равновесия химических реакций и закона Дальтона. Такая система уравнений расчета равновесного состава газовой смеси является нелинейной и требует многократного численного решения, поэтому является наиболее затратной процедурой. Проведено сравнение решения по полной нелинейной модели воздуха, состоящего из 11 компонент (e^-, N, O, Ar, N₂, O₂, NO, N⁺, O⁺, Ar⁺, NO⁺) и аналитической модели Крайко. Получено совпадение мольных долей компонентов смеси и термодинамических параметров в широком диапазоне изменения давления и температуры. При использовании аналитических аппроксимаций, вычислительные затраты значительно меньше. Зависимости состава воздуха от температуры приведены на рис. 1 при давлении, равном 1013.25 Па.

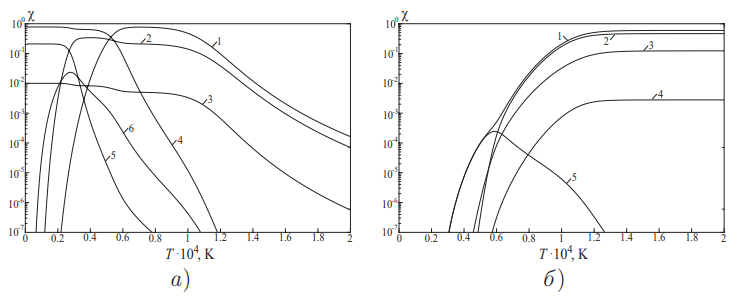
Рис. 1: Зависимость равновесного состава воздуха от температуры при давлении 0.01 атм. а) 1 — N, 2 — O, 3 — Ar, 4 — N₂, 5 — O₂, 6 — NO. б ) 1 — e, 2 — N⁺, 3 — O⁺, 4 — Ar⁺, 5 — NO⁺

Расчет течений производится с помощью метода конечных объемов. Расчетная область разделяется на множество контрольных объемов, для дискретизации производной по времени используется явная схема Рунге– Кутты третьего порядка. Для вычисления конвективных потоков на грани контрольного объема используются различные подходы (схема Роэ, Годунова, Русанова и т.д.), второй порядок аппроксимации по пространству достигается с помощью интерполяции из центра ячеек на грань конечного объема с функцией ограничения градиента решения для обеспечения монотонности схемы. Вязкая часть потока аппроксимируется по явной схеме.

Для приближенного учета сложных физико-химических процессов в реальных газах используется методология эффективного показателя адиабаты. Это обеспечивает создание универсального вычислительного комплекса, структурированного на ряд автономных сегментов, с возможностью независимой модификации их функционального наполнения, усовершенствование алгоритмов и компьютерной реализации. Для построения неструктурированных сеток используются различные открытые и коммерческие пакеты прикладных программ (Gmsh, Ansys ICEM CFD и другие). Для хранения данных о неструктурированной сетке используется формат OpenFOAM. Это позволяет использовать имеющиеся программные модули для обработки входных и выходных данных, также для управления расчетами на основе открытых кодов. Для ускорения расчетов основные вычисления выполняются на графических ускорителях. Для реализации алгоритма расчета на GPU используется технология CUDA. Разработанные алгоритмы тестировались на задачах имеющих аналитическое решение и задачах имеющих либо экспериментальные данные, либо расчеты других авторов.

В качестве практического применения расчетных методик рассматривается задача обтекание планера гиперзвукового летательного аппарата при нулевом угле атаки рис. 2 (реализованная модель приблизительно соответствует планеру гиперзвукового летательного аппарата Х-43). Условия расчета соответствуют числу Маха M = 10 на высоте 30 км, размеры планера выбираются равными 3.66×1.5 м². Давление воздуха на данной высоте полагается равным p = 1172 Па, а температура — T = 227 K. При заданных условиях скорость полета составляет V = 2976.62 м/с.

Задача решается в трехмерной постановке для половины расчетной области, размеры которой выбираются равными 6×4×2 м³. На входной границе задаются граничные условия сверхзвукового втекания в расчетную область, а на выходной границе — условия сверхзвукового вытекания. На стенке используются граничные условия прилипания и скольжения для скорости. Поверхность тела полагается теплоизолированной. Для расчета используется неструктурированная расчетная сетка, которая состоит из 16 миллионов ячеек и 48 миллионов граней.

Рис. 2: Общий вид планера.

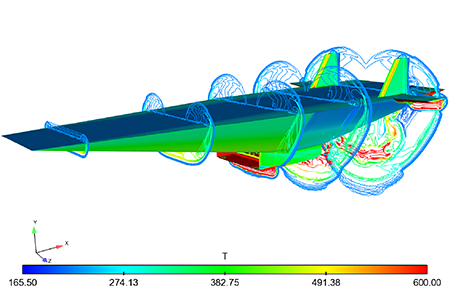
Распределение температуры на поверхности планера приводится на рис. 3. В поперечных сечениях представлены контуры градиента плотности, которые характеризуют положение скачков уплотнения. Наиболее высокая температура наблюдается на входе в воздухозаборник. На рис. 4 представлено распределение давления по поверхности ЛА и линии тока, которые показывают расположение вихрей.

Расчеты производились на различном оборудовании. На сервере 1 использовалось одно ядро центрального процессора Xeon E5-2680 v3 и один расчетный модуль NVidia Tesla K40, а на сервере 2 использовался один поток процессора IBM Power8 CPU и один расчетный модуль NVidia Tesla P100.

Для тестирования производительности на центральном процессоре реализован похожий алгоритм расчета по модели совершенного газа и с учетом химических реакций. Для сравнения, в таблице приведено время расчета с помощью пакета Ansys Fluent на аналогичной сетке и с похожими настройками (расчет потока по схеме Роэ). В табл. 1 приводится время выполнения одного шага по времени с осреднением по 10 итерациям для различных настроек расчетного модуля.

Таблица 1: Сравнение длительности выполнения шага по времени.